导数、微分、积分之间的区别与联系

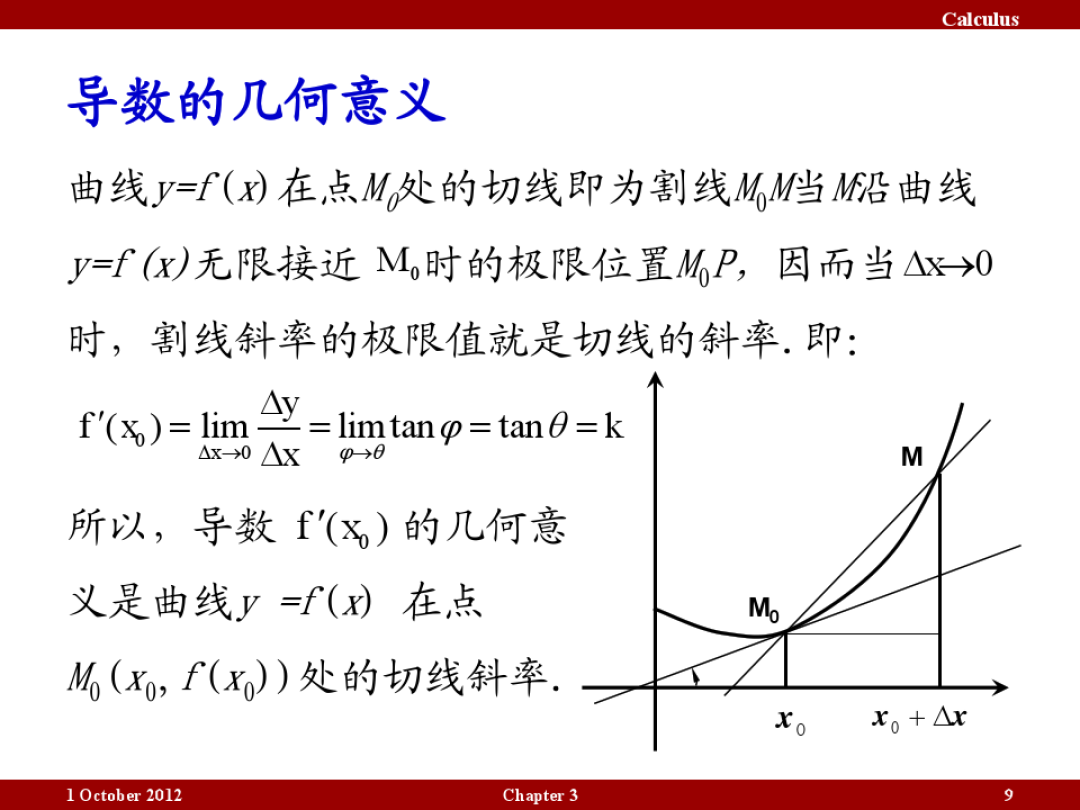
导数：曲线某点的导数就是该点切线的斜率，在物理学里体现了是瞬时速度，二阶导数则是加速度。这个是由牛顿提出并研究的方向。

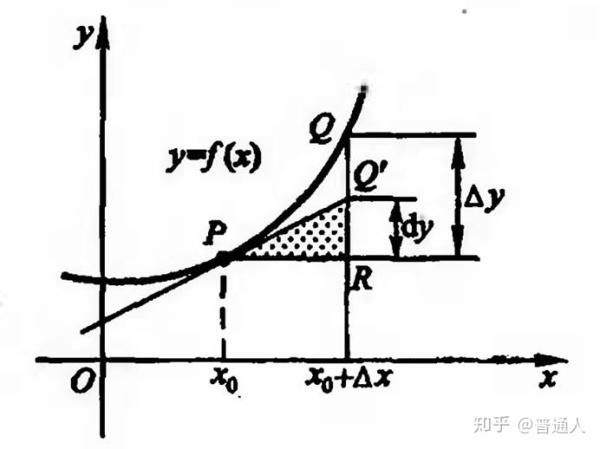
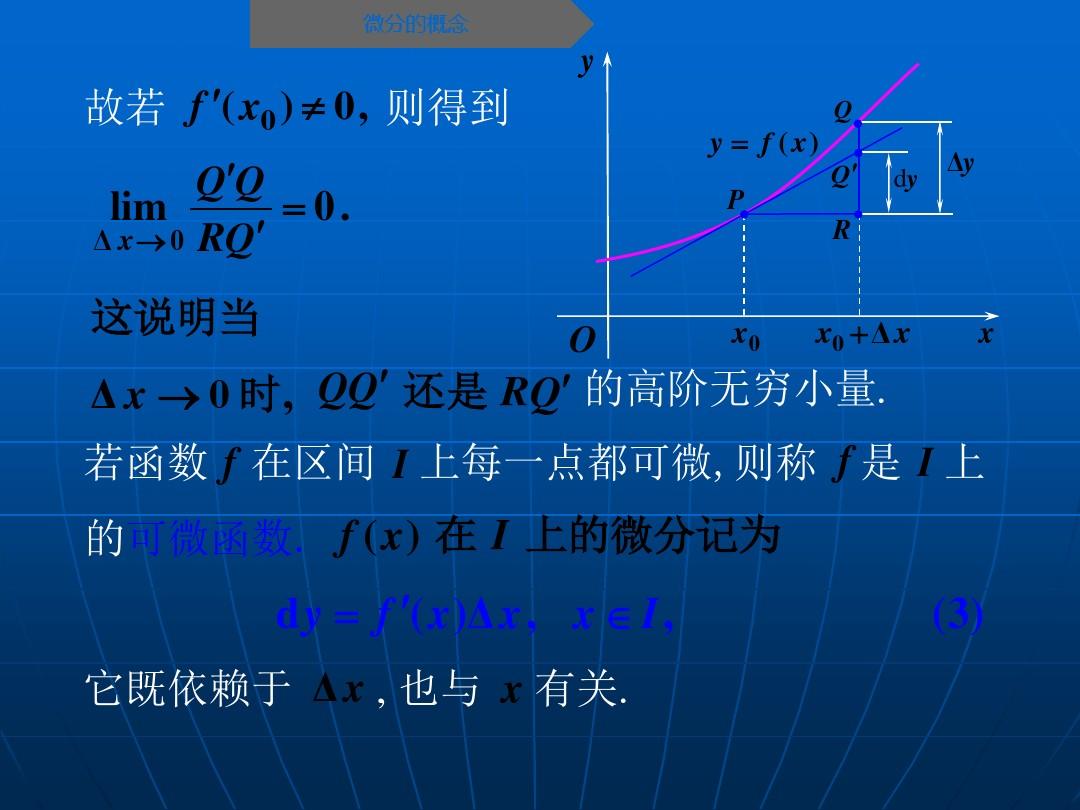
微分：也就是把函数分成无限小的部分，当曲线无限的被缩小后,可以近似当作直线对待,微分也就能表示为导数与dx的乘积。这个是莱布尼兹提出并研究的方向。

其实导数和微分本质上说并无区别，只是研究方向上的差异。

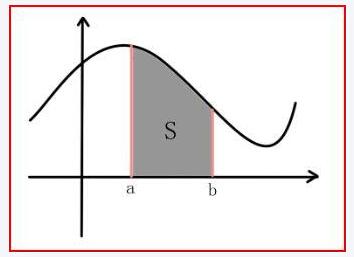
积分：定积分就是求曲线与x轴所夹的面积；不定积分就是该面积满足的方程式 ,因此后者是求定积分的一种手段,本质上来说,不定积分就是变限的定积分。

换一个角度来说：

导数y'是函数在某一点的变化率,微分是改变量,导数是函数微分与自变量微分之商,即y'=dy/dx,所以导数与微分的理论和方法统称为微分学（已知函数,求导数或微分）.积分则是微分学的逆问题。

极限是微分、导数、不定积分、定积分的基础,最初微积分由牛顿、莱布尼茨发现的时候,没有严格的定义,后来法国数学家柯西运用极限,使微积分有了严格的数学基础.极限是导数的基础,导数是极限的化简.微分是导数的变形。

微分：无限小块的增量可以看作是变化率，也就是导数。 积分：无限小块的面积和可以看作是整个面积。

可导必连续，闭区间上连续一定可积，可积一定有界。

拓展资料

导数

导数是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'(x0)或df(x0)/dx。 导数是函数的局部性质。

一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。

例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。 不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。然而，可导的函数一定连续；不连续的函数一定不可导。

对于可导的函数f(x)，x↦f'(x)也是一个函数，称作f(x)的导函数（简称导数）。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上，求导就是一个求极限的过程，导数的四则运算法则也来源于极限的四则运算法则。反之，已知导函数也可以倒过来求原来的函数，即不定积分。微积分基本定理说明了求原函数与积分是等价的。求导和积分是一对互逆的操作，它们都是微积分学中最为基础的概念。