从勾股定理到立方公式的整数解

从勾股定理到坐标

从数学上的垂直与乘法相照应的关系，我们发现具有直角的几何图形会具有一些与算术相对应的特殊性质，这其中最重要的就是勾股定理——a^2+b^2=c^2。

这个小学必学的知识，其本质来源于面积，下面这张图可以清晰地让人理解到底是为什么。

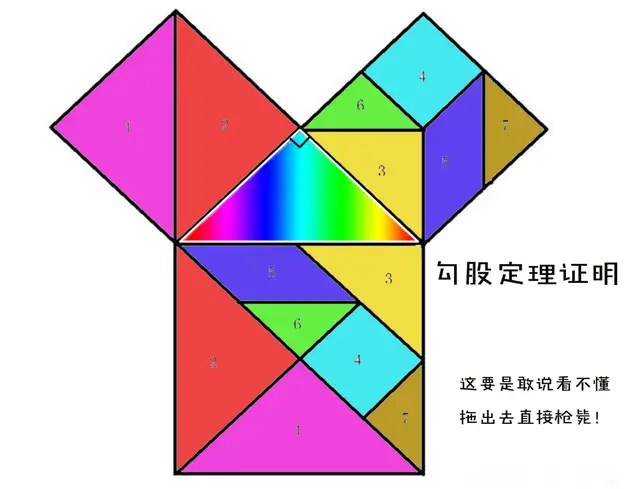
现在让将勾股定理的方程稍加改造，得到一个二元方程：x^2+y^2=1^2

什么是方程？一方程其实就是关系的表征，比如上面这个方程，是用勾股定理改造出来的。所以我们同样可以将它以二维平面面积的方式来理解。直角三角形其实就是长方形的两条边与一条对角线，所以将x和y作为长度来看，这个方程就可以解析成“在对角线长度固定的情况下，所有满足条件的长方形边长关系”。

把这些长方形都画出来，如果这些长方形对角线的一端重合，那么另一端的点就会构成一个弧形。在这个弧形中每个点到重合点的距离都为1，也就是所谓的圆，上面这个方程也就变成了圆的方程。

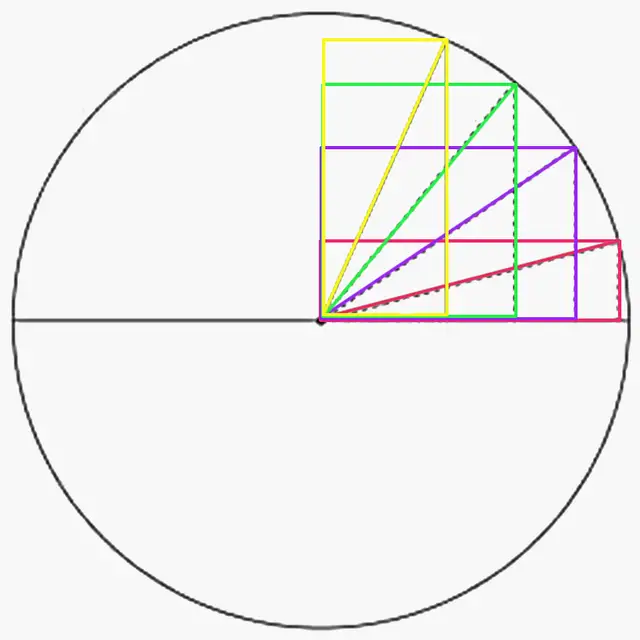
通过上面的分析我们可以得到一个概念，那就是“坐标”，用两个边长去确定由它构成的直角三角形的顶点。我们现在得到了两个“参数”与一个“规律”，用它们组成的数学式子就是“方程”。

为什么要从二维升到三维

那么现在让我们进入三维世界吧，不过不是我们熟悉的那种进入，而是从简单粗暴地直接把圆的方程进行扩展，把x^2+y^2=1^2变成x^2+y^2+z^2=1^2会得到什么呢？答案是球面的方程，这个方程的意思是：在立方体的对角线长度为1的情况下，所有满足条件的立方体相互间的边长关系。

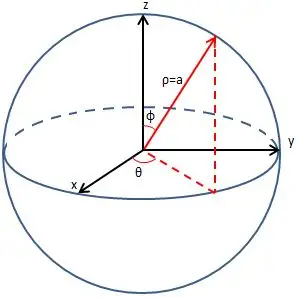
数学家的操作——加一维

平方公式与立方公式。

ax十bX十cX十D=0。

这一方程公式，用任一自然整数代入，它的解一定是整数，这是确定无疑的。那么。

a^2十b^2=c^2

a^3十b^3十c^3=e^3。

而上面的平方公式和立方公式，甪任一自然整数代入，它的解就不一定是整数了。而有整数解的数只有很少一部分了。但代入怎样的自然整数才能使它们成为整数。我们有。

3^2十4^2=5^2=25。

3^3十4^3十5^3=6^3=2l6。

（2X3）^2十（2X4）^2=（2X5）^2=100。

（2x3）^3十（3x4）^3十（3X5）^3=（3X6）^3=1728。

（3x3）^2十（3x4）^2=（3X5）^2=225。

（3X3）^3十（3x4）^3十（3X5）^3=（3X6）^2=5832。

。。。。。。

由此可知：

3X^2十4X^2=5X^2

3X^3十4X^2十5X^3=6X^3。

就这样，从平方整数解公式到立方解整数公式就这样完成了。那么，这个立方整数解公式是一个什么样的球呢？那只有请一个农村老大娘给你用纸糊一个小朋友的钱罐子了。

所以对于勾股定理，有勾三股四弦五的说法，那么，对于立方整数解的公式应该有一个怎么样的说法呢。

好，到这儿为止都是我们可以轻松理解的东西，现在请你再看看圆与球的两个方程，如果你是数学家，你是不是觉得似乎可以顺水推舟地再做一些什么呢？

比如……再给它加个参数试试？整个x^2+y^2+z^2+w^2=1^2出来看看？

这个式子在算术上很好理解，四个参数，相互间满足一定的关系。

但是根据之前方程可以依托面积或体积照射到现实世界中的规律来看，我们是不是也可以将这个方程画出来呢？

不能……因为在我们生存的宏观世界，体积是空间的基本单位，不存在什么东西用三维无法描述，上文中强调的“存在先行”指出没有需要的维度是没有意义的，加入这个维度我们也找不到需要用它来描述的东西。

但是我们可以对其进行想象与计算，在数学上它与二维或是三维是平等的，所以数学家们当然不可能拒绝它。

这，就是所谓的四维空间。